Introduction
In this blog post, I want to introduce the fork/join framework that has been part of Java since version 7. In order to demonstrate its great advantages, I set up a scenario of lengthy calculations. This article will compare its trivial single thread computation, a parallel computation using a fixed thread pool, and finally two ways of using the fork/join framework.
Lengthy Computation and Timestamped Values
The examples of the fork/join framework I’ve seen in the German popular Java literature so far aren’t very convincing. Calculating factorial or Fibonacci numbers the recursive way and then optimizing them using fork-join algorithms simply fixes artificial problems that shouldn’t have been introduced in the first place. The same applies to multiplying large numbers by repeatedly adding them. What I’m missing in all these examples is the really long calculations. Thus, first let me introduce some lengthy calculations:
import java.util.concurrent.*;
public final class LengthyComputation {
private static final int SEQUENCE_LENGTH
= 10_000;
/* Multiplier for linear congruential generator, taken from "Numerical Recipes". */
private static final int A
= 1_664_525;
/* Increment for linear congruential generator, taken from "Numerical Recipes". */
private static final int C
= 1_013_904_223;
private LengthyComputation() {}
public static int computeValue(int passCount) {
int value = ThreadLocalRandom.current().nextInt();
/* Compute linear congruential generator sequences of length passCount * SEQUENCE_LENGTH. */
for (int passNumber = 1; passNumber <= passCount; passNumber++) {
for (int valueNumber = 1; valueNumber <= SEQUENCE_LENGTH; valueNumber++) {
value = A * value + C;
}
}
return value;
}
}The class LengthyComputation will be used by all code examples below. It contains a single static method computeValue(int passCount) that computes a single number by applying a linear congruential generator (LCG) 10,000 times. Actually, an LCG is a common way of generating so-called pseudo-random numbers. As the name implies, the numbers are not random at all, but at least they “look” random. I chose to implement an LCG because it provides an easy way of performing “endless” calculations. There is no risk of any numerical overflows or underflows that make the calculations useless, as do, e.g., factorials or Fibonacci numbers. (Actually, for the LCG it happens all the time, but that’s the way it’s supposed to be.) By passing a positive number for passCount, the caller can control how long that calculation will last. E.g., the method call computeValue(1000) will compute 10 times longer than the method call computeValue(100).
For real-world applications, simply replace LengthyComputation by your own lengthy computation.
In order to observe the behavior of the different computation styles presented in this article, the scenarios will always consist of filling an array with 10,000 values obtained by those lengthy calculation just explained above. In addition, each computed value is stored together with a timestamp that contains the total time that has passed from the start until the value has been computed. The corresponding data structure is trivial:
import java.time.*;
import java.util.*;
public final class TimestampedValue {
private int value;
private Duration timestamp;
public TimestampedValue(int value, Duration timestamp) {
/* Check and adopt parameters. */
Objects.requireNonNull(timestamp);
this.value = value;
this.timestamp = timestamp;
}
public int getValue() {
return value;
}
public Duration getTimestamp() {
return timestamp;
}
}There is one more important thing: If each of the 10,000 array values were calculated the same way, each of the 10,000 computations would need more or less the same amount of time. This is probably not very realistic in real world, where problem sizes usually differ. It also doesn’t demonstrate the advantage of the fork/join framework, because it probably wouldn’t perform better than simply splitting the array into n pieces and let n independent threads perform the work in parallel (where n usually should be the number of CPU cores).
Thus, the calculation of the array element at index 0 will perform 0 passes inside the computeValue method, the calculation of the array element at index 5000 will perform 5000 passes, and the calculation at index 9999 will perform 9999. Filling the array with 10,000 computed values will thus be very asymmetric, since computing values at higher indexes will take longer than computing values at lower indexes.
Single Thread Computation
The following class SingleThreadComputation computes all 10,000 elements of the valueArray the trivial way. It consists of a single thread. A simple loop iterates through all indexes from 0 to 9999, calls the computeValue method (using arrayIndex as the pass count, as explained in the section above), and stores its value together with the current timestamp. If PRINT_MESSAGES = true, then you can see the progress of filling the array. At the beginning, it’s pretty fast, while continuously slowing down throughout the whole range. Here is the code:
import java.time.*;
public final class SingleThreadComputation {
private static final boolean PRINT_MESSAGES
// = false;
= true;
private static final int VALUE_ARRAY_SIZE
= 10_000;
private TimestampedValue[] valueArray
= new TimestampedValue[VALUE_ARRAY_SIZE];
public static void main(String[] args) {
SingleThreadComputation computation = new SingleThreadComputation();
computation.compute();
// computation.printTimestamps();
}
private void compute() {
Instant startTime = Instant.now();
for (int arrayIndex = 0; arrayIndex < VALUE_ARRAY_SIZE; arrayIndex++) {
/* Print message, if enabled. */
if (PRINT_MESSAGES) {
if ((arrayIndex % 10) == 0) {
System.out.format("Computing values for indexes %4d to %4d.%n",
Integer.valueOf(arrayIndex),
Integer.valueOf(Math.min(arrayIndex + 9,
VALUE_ARRAY_SIZE - 1)));
}
}
/* Compute and save timestamped value. */
int value = LengthyComputation.computeValue(arrayIndex);
Duration timestamp = Duration.between(startTime, Instant.now());
valueArray[arrayIndex] = new TimestampedValue(value, timestamp);
}
}
private void printTimestamps() {
for (int arrayIndex = 0; arrayIndex < VALUE_ARRAY_SIZE; arrayIndex++) {
System.out.println(arrayIndex + "\t"
+ valueArray[arrayIndex].getTimestamp().toMillis());
}
}
}On my machine (MacBook Pro with a 2.8 GHz Intel Core i7 CPU), the whole computation takes about 566 s, i.e., about 9.4 min. The following figure shows the timestamps of each valueArray element, perfectly illustrating the parabolic total time behavior of the linearly increasing single element computation durations:
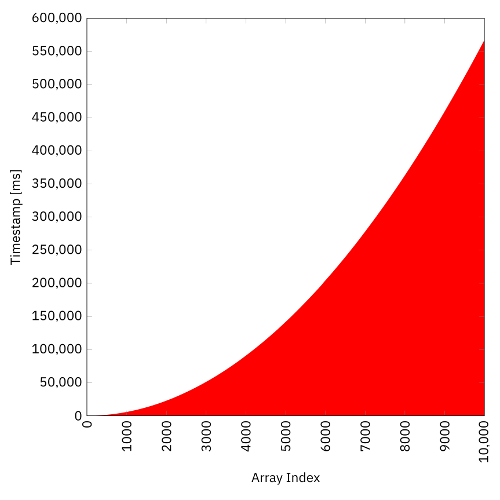
In order to reproduce all of the diagrams shown in this article, you can uncomment the corresponding method calls computation.printTimestamps(). They print an unformatted list of array-index/timestamp pairs. When you forward their console output to files and then use any plot tool of your choice, you will get similar results.
Fixed Thread Pool Computation
With the Concurrency Utilities, introduced in Java 5, came several kinds of thread pools. They make manual handling with threads obsolete. Instead of tweaking with wait, notify, and notifyAll, one better uses one of the thread pools provided. Such a pool contains—in its basic form—a queue that contains all submitted tasks (a “to-do list” of tasks) and has several so-called worker threads that take the jobs from the queue and execute them. The main advantage is its ability to reuse its worker threads, thus eliminating most of the overhead that occurs when creating and removing threads.
The number of worker threads can be either fixed or dynamic, depending on the type of thread pool. Executors.newFixedThreadPool(int) returns an ExecutorService with a fixed number of threads. Ideally, one sets the number of worker threads equal to the number of CPUs in the system (hyper-threading CPU cores count twice). The method call Runtime.getRuntime().availableProcessors() always returns the correct number.
In order to speed up the computation of all valueArray values, the code example below splits the array into THREAD_COUNT (on my machine, 8) subarrays and then submits computation tasks to the thread pool, where each task computes (on my machine) 1/8th of the array. Here is the code:
import java.time.*;
import java.util.concurrent.*;
public final class FixedThreadPoolComputation {
private static final int VALUE_ARRAY_SIZE
= 10_000;
private static final int THREAD_COUNT
= Runtime.getRuntime().availableProcessors();
private TimestampedValue[] valueArray
= new TimestampedValue[VALUE_ARRAY_SIZE];
private Instant startTime;
public static void main(String[] args)
throws InterruptedException {
FixedThreadPoolComputation computation = new FixedThreadPoolComputation();
computation.setUpAndSubmitComputation();
// computation.printTimestamps();
}
private void setUpAndSubmitComputation()
throws InterruptedException {
startTime = Instant.now();
/* Submit equally sized subarrays to a fixed thread pool, one for each thread. */
ExecutorService service = Executors.newFixedThreadPool(THREAD_COUNT);
for (int threadNumber = 1; threadNumber <= THREAD_COUNT; threadNumber++) {
final int indexMinInclusive = VALUE_ARRAY_SIZE * (threadNumber - 1) / THREAD_COUNT;
final int indexMaxExclusive = VALUE_ARRAY_SIZE * threadNumber / THREAD_COUNT;
service.submit(() -> compute(indexMinInclusive, indexMaxExclusive));
}
/* Shut down executor service and wait for all submitted threads to finish. */
service.shutdown();
while (!service.awaitTermination(1, TimeUnit.MINUTES)) {}
}
private void compute(int indexMinInclusive, int indexMaxExclusive) {
for (int arrayIndex = indexMinInclusive; arrayIndex < indexMaxExclusive; arrayIndex++) {
/* Compute and save timestamped value. */
int value = LengthyComputation.computeValue(arrayIndex);
Duration timestamp = Duration.between(startTime, Instant.now());
valueArray[arrayIndex] = new TimestampedValue(value, timestamp);
}
}
/* [...] Method printTimestamps() omitted. */
}If all elements needed the same amount of computing time, then the array would be filled in about 1/8th of the time. As I’ve stated earlier, computing times increase with increasing indexes. So the 8th thread, computing the values for the indexes from 8750 to 9999, has much more work to do than the 1st thread, computing from index 0 to 1249. The diagram below confirms this assumption:
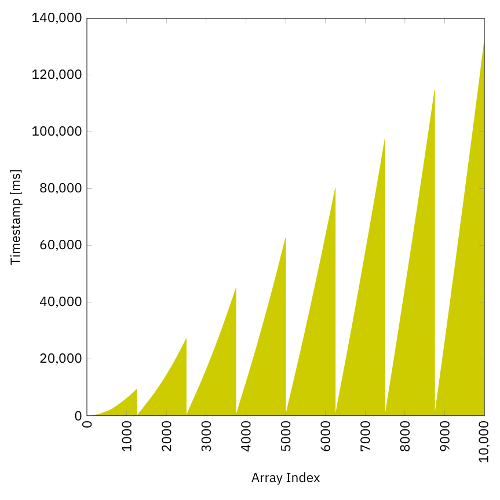
The total time using the fixed thread pool on my machine is 132 s, i.e., 2.2 min, and thus more than 4 times faster than the single thread computation from the previous section.
Fork/Join Pool | Invoke-All Computation
A fork/join pool is a thread pool that is designed for tasks being split, thus following a divide and conquer strategy. If a problem is too large (as filling an array with 10,000 computed values definitely is), it is split into (usually) two smaller pieces. So if filling the valueArray with 10,000 elements is complicated, probably filling the array with “only” 5000 elements isn’t? Well, it still is, but if the problem size is divided further and further, one finally arrives at a point where solving the problem becomes trivial. This is definitely the case if there is just one valueArray element left to be computed, but for the sake of perfomance optimization, let’s assume that computing 10 elements can be regarded trivial as well.
Below is the first part of the code, the InvokeAllComputationAction, extending Java’s RecursiveAction:
import java.time.*;
import java.util.*;
import java.util.concurrent.*;
@SuppressWarnings("serial")
public final class InvokeAllComputationAction extends RecursiveAction {
private static final boolean PRINT_MESSAGES
// = false;
= true;
private static final int BASE_CASE_ELEMENT_COUNT_MAX
= 10;
private static TimestampedValue[] valueArray;
private static Instant startTime;
private int indexMinInclusive;
private int indexMaxExclusive;
public InvokeAllComputationAction(int indexMinInclusive, int indexMaxExclusive,
TimestampedValue[] valueArray, Instant startTime) {
this(indexMinInclusive, indexMaxExclusive);
/* Check and adopt remaining parameters. */
Objects.requireNonNull(valueArray);
Objects.requireNonNull(startTime);
InvokeAllComputationAction.valueArray = valueArray;
InvokeAllComputationAction.startTime = startTime;
}
public InvokeAllComputationAction(int indexMinInclusive, int indexMaxExclusive) {
/* Adopt parameters. */
this.indexMinInclusive = indexMinInclusive;
this.indexMaxExclusive = indexMaxExclusive;
}
@Override
protected void compute() {
/* base case */
if ((indexMaxExclusive - indexMinInclusive) <= BASE_CASE_ELEMENT_COUNT_MAX) {
/* Print message, if enabled. */
if (PRINT_MESSAGES) {
System.out.format("Computing base case for indexes %4d to %4d.%n",
Integer.valueOf(indexMinInclusive),
Integer.valueOf(indexMaxExclusive - 1));
}
for (int arrayIndex = indexMinInclusive;
arrayIndex < indexMaxExclusive;
arrayIndex++) {
/* Compute and save timestamped value. */
int value = LengthyComputation.computeValue(arrayIndex);
Duration timestamp = Duration.between(startTime, Instant.now());
valueArray[arrayIndex] = new TimestampedValue(value, timestamp);
}
/* recursive case */
} else {
int indexMid = (indexMinInclusive + indexMaxExclusive) / 2;
/* Print message, if enabled. */
if (PRINT_MESSAGES) {
System.out.format("Invoking recursive cases for indexes %4d to %4d "
+ "and %4d to %4d.%n",
Integer.valueOf(indexMinInclusive),
Integer.valueOf(indexMid - 1),
Integer.valueOf(indexMid),
Integer.valueOf(indexMaxExclusive - 1));
}
/* Invoke recursive computation action for both subarrays. */
invokeAll(new InvokeAllComputationAction(indexMinInclusive, indexMid),
new InvokeAllComputationAction(indexMid, indexMaxExclusive));
}
}
}The whole concept is based on recursion. The base case is the trivial case that can be computed directly, as explained above. Its threshold can be set by the constant BASE_CASE_ELEMENT_COUNT_MAX, which is initially set to 10. (You won’t recognize significant differences for all values between 1 to 100, because the actual computation time of the values is significantly longer than the overhead time for additional loops or method calls.)
The recursive case represents the “complicated” case. The current subarray (actually it’s just a “window” represented by the indexes indexMinInclusive and indexMaxExclusive) is split into two halves. Two InvokeAllComputationActions are then created, each representing a computation task for one of the two halves (again, by simply storing their window indexes). The invokeAll call at the very bottom of the code then enqueues these two tasks.
Fork/join pools are optimized in their way they process enqueued tasks. Each worker thread has its own local queue, in addition to a single global queue. Each worker thread first works through its own local task queue. If one worker thread has emptied its own queue, it applies work stealing, i.e., it “steals” work from another local queue.
The invokeAll call causes new tasks to be put in a thread’s own local queue. Tasks from a thread’s own local queue are dequeued in LIFO order (i.e., the latest task comes first, like a stack), tasks from a different thread’s local queue are dequeued in FIFO order (i.e., the oldest task comes first, like a pipeline). The latter also applies to the global queue that is dequeued if the worker threads can no longer steal work from other threads.
The concept described above has several advantages. Imagine that the “youngest” tasks are usually the smallest ones. They should be dealt with first (in a recursive manner), thus the LIFO (stack) order for local tasks. When performing work stealing from other local queues, it makes sense to grab the “largest” tasks, which are probably the oldest in the queue, thus the FIFO (pipeline) order. The same applies to the global queue (the oldest task will probably be the longest).
The code above only represents the actual computation part. The code below shows the main class, initializing the fork/join pool and the computation action:
import java.time.*;
import java.util.concurrent.*;
public final class ForkJoinPoolInvokeAllComputation {
private static final int VALUE_ARRAY_SIZE
= 10_000;
private TimestampedValue[] valueArray
= new TimestampedValue[VALUE_ARRAY_SIZE];
public static void main(String[] args)
throws InterruptedException {
ForkJoinPoolInvokeAllComputation computation = new ForkJoinPoolInvokeAllComputation();
computation.setUpAndInvokeComputation();
// computation.printTimestamps();
}
private void setUpAndInvokeComputation()
throws InterruptedException {
Instant startTime = Instant.now();
/* Set up fork/join pool and invoke recursive computation action for whole array. */
ForkJoinTask<Void> action
= new InvokeAllComputationAction(0, VALUE_ARRAY_SIZE, valueArray, startTime);
ForkJoinPool pool = new ForkJoinPool();
pool.invoke(action);
}
/* [...] Method printTimestamps() omitted. */
}The timestamp diagram shows that there has been another significant speedup:
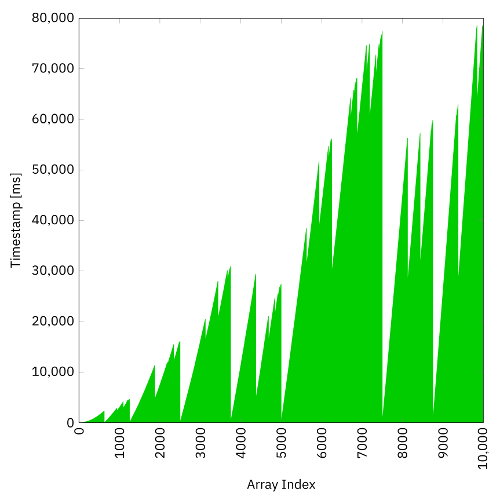
The whole computation is now finished within 79 s, which is about 40 % faster than the fixed thread pool computation from the previous section, and more than 7 times faster than the single thread computation. This is due to the fact that threads with no more work to do—which the lower index threads usually have more often than the higher index threads—will help out doing work that was initially assigned to different worker threads. The whole behavior also explains the “chaotic” pattern of the diagram.
Fork/Join Pool | Fork-Join Computation
The previous section has used the fork/join framework, however, there haven’t been any explicit fork or join calls. The invokeAll method causes both subtasks to be enqueued. This is fine, but won’t help if we want to obtain results from a computation of a subtask.
The code example below uses the explicit fork-join mechanism in order to calculate the sum of all valueArray elements—of course recursively:
import java.time.*;
import java.util.*;
import java.util.concurrent.*;
@SuppressWarnings("serial")
public final class ForkJoinComputationTask extends RecursiveTask<Long> {
/* [...] Fields and constructors omitted. */
@Override
protected Long compute() {
/* base case */
if ((indexMaxExclusive - indexMinInclusive) <= BASE_CASE_ELEMENT_COUNT_MAX) {
/* Print message, if enabled. */
if (PRINT_MESSAGES) {
System.out.format("Computing base case for indexes %4d to %4d.%n",
Integer.valueOf(indexMinInclusive),
Integer.valueOf(indexMaxExclusive - 1));
}
long valueSum = 0;
for (int arrayIndex = indexMinInclusive;
arrayIndex < indexMaxExclusive;
arrayIndex++) {
/* Compute and save timestamped value, update value sum. */
int value = LengthyComputation.computeValue(arrayIndex);
Duration timestamp = Duration.between(startTime, Instant.now());
valueArray[arrayIndex] = new TimestampedValue(value, timestamp);
valueSum += value;
}
return Long.valueOf(valueSum);
/* recursive case */
} else {
int indexMid = (indexMinInclusive + indexMaxExclusive) / 2;
/* Print messages, if enabled. */
if (PRINT_MESSAGES) {
System.out.format("Forking recursive case for indexes %4d to %4d.%n",
Integer.valueOf(indexMinInclusive),
Integer.valueOf(indexMid - 1));
System.out.format("Computing recursive case for indexes %4d to %4d.%n",
Integer.valueOf(indexMid),
Integer.valueOf(indexMaxExclusive - 1));
}
/*
* Fork recursive computation task for first subarray,
* directly compute task for second subarray.
*/
ForkJoinComputationTask forkedTask
= new ForkJoinComputationTask(indexMinInclusive, indexMid);
ForkJoinComputationTask currentTask
= new ForkJoinComputationTask(indexMid, indexMaxExclusive);
forkedTask.fork();
long currentTaskValueSum = currentTask.compute().longValue();
long forkedTaskValueSum = forkedTask.join().longValue();
return Long.valueOf(currentTaskValueSum + forkedTaskValueSum);
}
}
}Note that the ForkJoinComputationTask now extends RecursiveTask<Long> instead of RecursiveAction. RecursiveTask’s compute method returns a value, while RecursiveAction’s method does not.
The base case calculates and returns the value sum of its trivial case. The recursive case logically splits its (large) subarray window into two halves. The first half is being forked, i.e., it is enqueued such that another thread can steal this task. Forking kind of means putting it away and expecting a parallel worker thread to deal with it. In the meantime, the current thread computes the other half itself, i.e., it does the computation in its own thread. Now in order to calculate the total sum of the whole subarray, the worker thread needs to wait for the other (the first) half to finish. This is done by calling the blocking method join. Since both subtasks are expected to be more or less of the same length, joining probably doesn’t block too long. As soon as both “half sums” are ready, the method adds both parts and returns the total.
Below you find the main class for the real fork-join computation:
import java.time.*;
import java.util.concurrent.*;
public final class ForkJoinPoolForkJoinComputation {
private static final int VALUE_ARRAY_SIZE
= 10_000;
private TimestampedValue[] valueArray
= new TimestampedValue[VALUE_ARRAY_SIZE];
public static void main(String[] args)
throws InterruptedException {
ForkJoinPoolForkJoinComputation computation = new ForkJoinPoolForkJoinComputation();
long valueSum = computation.setUpAndInvokeComputation();
// computation.printTimestamps();
computation.checkAndPrintValueSums(valueSum);
}
private long setUpAndInvokeComputation()
throws InterruptedException {
Instant startTime = Instant.now();
/* Set up fork/join pool and invoke recursive computation task for whole array. */
ForkJoinTask<Long> task
= new ForkJoinComputationTask(0, VALUE_ARRAY_SIZE, valueArray, startTime);
ForkJoinPool pool = new ForkJoinPool();
long valueSum = pool.invoke(task).longValue();
return valueSum;
}
/* [...] Method printTimestamps() omitted. */
private void checkAndPrintValueSums(long forkJoinValueSum) {
/* Sum up all values of value array. */
long arrayValueSum = 0;
for (int arrayIndex = 0; arrayIndex < VALUE_ARRAY_SIZE; arrayIndex++) {
arrayValueSum += valueArray[arrayIndex].getValue();
}
System.out.format("Fork/Join Value Sum: %d%nArray Value Sum: %d%n",
Long.valueOf(forkJoinValueSum), Long.valueOf(arrayValueSum));
}
}There is also a method that calculates the valueArray sum by iterating through all elements. This is simply a test method in order to check if the results from the fork-join algorithms are correct.
The timestamp diagram looks slightly different, but still results in the same total execution time as before. Which half of the array is computed by another thread and which half is calculated by the own thread doesn’t matter and is just a matter of personal preference.
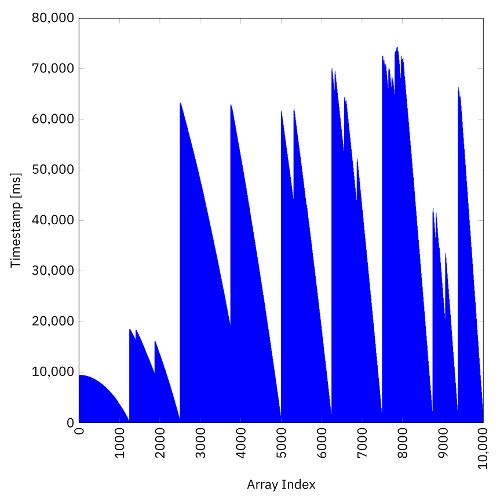
Conclusion
The following figure puts all four scenarios into a single diagram:
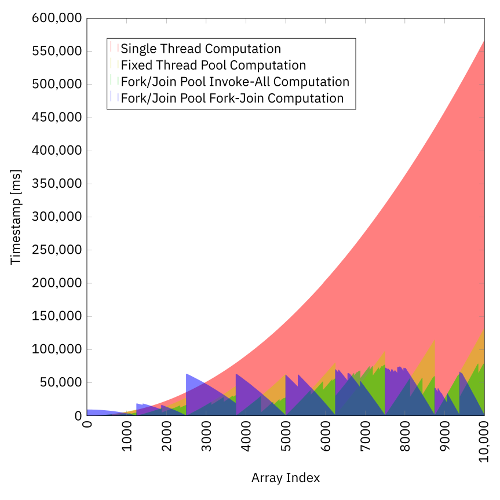
The nature of the problem makes the fork/join framework perform best. Due to the unequal computing times for the array values, simply splitting the whole task into n subtasks and letting them perform in parallel doesn’t perform as well. However, its source code is significantly shorter.
The lesson is clear: in concurrency, there is no one-size-fits-all solution. One first needs to understand the underlying problem before applying the (hopefully simplest) algorithm. The fork/join framework is very flexible and can adjust itself to “asymmetric” situations perfectly. However, it comes with the cost of more boilerplate code. Hopefully, this blog post can be of help when implementing an own fork-join computation in the future.
Shortlink to this blog post: link.simplexacode.ch/529z2019.01
